师徒两人合作完成一项工程，由于配合得好，师傅的工作效率比单独做时要提高亩，徒弟的工作效率比单独做时提高1/5。两人合作6天，完成全部工程的2/5，接着徒弟又单独做6天，这时这项工程还有13/30完成，如果这项工程由师傅一人做，几天能完成?A.27 B.30 C.33 D.36

题目
师徒两人合作完成一项工程，由于配合得好，师傅的工作效率比单独做时要提高亩，徒弟的工作效率比单独做时提高1/5。两人合作6天，完成全部工程的2/5，接着徒弟又单独做6天，这时这项工程还有13/30完成，如果这项工程由师傅一人做，几天能完成?

A.27
B.30
C.33
D.36
相似考题

1.：一项工程，甲、乙、丙三人合做需要13小时完成。如果丙休息2小时，乙就要多做4小时，或者由甲、乙两人合做多做1小时，求这项工程由甲单独做要多少小时完成？（ ）A．24B．26C．30D．32

2.一项工作，甲单独做10田完成，乙单独做15田完成。问两人合作3天完成工作的几分之几？ A、1/2 B、1/3 C、1/5 D、1/6

3.有甲、乙两项工程，张师傅单独完成甲工程需要9天，单独完成乙工程需要12天；王师傅单独完成甲工程需要3天，单独完成乙工程需要15天。如果两人合作完成这两项工程，最少需要（ ）天。A．8B．10C．12D．14

4.：师徒两人加工一批零件，由师傅单独做需37小时，徒弟每小时能加工30个零件，现由师徒两人同时加工，完成任务时，徒弟加工的个数是师傅的59，这批零件共有()个。A.2060 B.2004 C.1998 D.2001

更多“师徒两人合作完成一项工程，由于配合得好，师傅的工作效率比单独做时要提高亩，徒弟的工作效率比单独做时提高1/5。两人合作6天，完成全部工程的2/5，接着徒弟又单独做6天，这时这项工程还有13/30完成，如果这项工程由师傅一人做，几天能完成?”相关问题

  • 第1题：

    有一工程，若由甲、乙单独做，分别需要12天和18天完成。若两人合做，因配合不默契，甲的工作效率比原来降低1／3，乙的工作效率比原来降低1／4，现在要求11天完成该工程，问两人至少需要合做多少天？

    A．3

    B．4

    C．5

    D．6


    正确答案：D

  • 第2题：

    师徒三人合作承包一项工程，4天能够全部完成．已知师傅单独做所需要的天数与毳个徒弟合作所需要的天数相等，师傅与甲徒弟合作所需天数的2倍与乙徒弟单独完成这项工程所需的天数相等．那么甲徒弟单独做，完成这项工程需要多少天？( )

    A．12

    B．18

    C．20

    D．24


    正确答案：D
    D[解析]根据“师徒合作四天能够完成”可知师徒三人合作的工作效率是1/4，根据“师傅单独完成与两徒弟合作完成这项工程的时间相等”可知师傅的工作效率是1/8；根据“师傅与甲徒弟合作所需天数的2倍与乙徒弟单独完成这项工程所需的天数相等”可知师徒三人合作的工作效率是乙徒弟的工作效率的3倍，所以乙徒弟的工作效率为1/4÷3=1/12，甲徒弟的工作效率为1/4 -1/8-1/12=1/24，故需要24天完成。

  • 第3题：

    一项工作，甲单独做15天完成，乙单独做12天完成。问：两人合作5天完成工作的几分之几？( )


    答案：D
    解析：
    工程问题。赋值工作总量为60，则甲的效率为4，乙的效率为5，两人合作5天完成5×（4+5）=45，完成工作的比例为。故本题选择D。

  • 第4题：

    甲、乙合作完成一项工作，由于配合得好，甲的工作效率比独做时提高了1/10,乙工作效率 比独做时提高了1/5,甲、乙两人合作4小时，完成全部工作的2/5.第二天乙又独做了 4小时，还剩下这件工作的13/30没完成。这项工作甲独做需要几个小时才能完成？（ ）

    A. 16
    B. 8
    C. 22
    D. 30

    答案：C
    解析：
    乙独做4小时完成全部工程的1一2/5-13/30=1/6,则乙独做时甲的工作效率为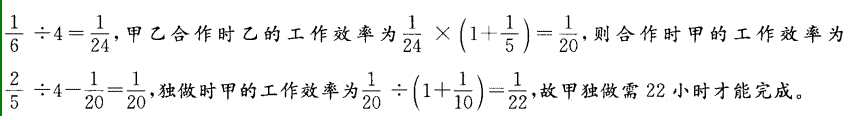

  • 第5题：

    一项工程甲、乙、丙一起来做，已知若甲、乙两人一起做则15天可以完成，若乙、丙两人一起做18天可以完成。已知在甲、乙、丙一起做这项工程的过程中，乙因事请假2天，结果共用10天恰好完成。那么这项工程若由乙单独做，要多少天完成？（ ）

    A. 36
    B. 48
    C. 54
    D. 56

    答案：C
    解析：
    本题可采用方程法。设整个工程的工作量为1，甲、乙、丙每天的工作量分别为x、y、z。根据题意可得：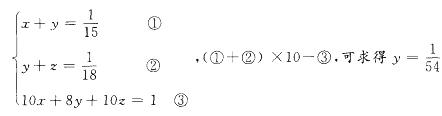

    即若乙单独做这项工程需要54天。

  • 第6题：

    甲、乙、丙三人共同完成一项工程，他们的工作效率之比是5:4:6。先由甲、乙两人合做6天，再由乙单独做9天，
    完成全部工程的60%。若剩下的工程由丙单独完成，则丙所需要的天数是

    A.9
    B.11
    C.10
    D.15

    答案：C
    解析：
    直接赋效率，已完成6*（5+4）+4*9=90，占60%，说明还剩60的工作量，60/6=10

  • 第7题：

    甲工程队与乙工程队的效率之比为4:5，一项工程由甲工程队单独做6天，再由乙工程队单独做8天，最后由甲、乙两个工程队合作4天刚好完成，如果这项工程由甲工程队或乙工程队单独完成，则甲工程队所需天数比乙工程队所需天数多多少天？

    A.3
    B.4
    C.5
    D.6

    答案：C
    解析：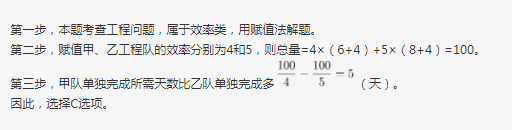

  • 第8题：

    一项工程，甲先单独做2天，然后与乙合做7天，这样才能完全工程的一半，已知甲、乙工效的比是2:3,如果这项工程由乙单独做,需要（ ）天才能完成

    A.24
    B.25
    C.26
    D.27
    E.28

    答案：C
    解析：

  • 第9题：

    甲、乙两队合作一项工程，按原来的工作效率，甲队单独完成比乙队单独完成少用了3天；现在甲队提高工效20％，乙队提高工效25％；这样甲队单独完成只比乙队单独完成少用2天。如果工作效率提高后，先由乙队单独做1天，然后两队合作，还需多少天完成?

    A.4
    B.5
    C.6
    D.7

    答案：B
    解析：
    设按原来的工作效率甲单独完成需要x天，则乙单独完成需要(x+3)天，提高效率后，甲

  • 第10题：

    师徒二人合作完成一批零件，需要6小时40分钟完成，且师傅每分钟比徒弟多完成1 个零件。若师傅一个人单独做，需要10小时完成所有零件。问这批零件共有多少个？

    A.1200
    B.1800
    C.2400
    D.3600

    答案：A
    解析：

  • 第11题：

    单选题
    某工程由甲单独做63天，再由乙单独接着做28天可以完成，如果甲乙两人合做需48天完成，现在甲先单独做42天，然后再由乙单独接着做，还需多少天可以完成？（　　）
    A

    56

    B

    60

    C

    74

    D

    85


    正确答案： B
    解析：
    设甲每天做工程的x，乙每天做工程的y，则有方程48x＋48y＝1，63x＋28y＝1，x＝1/84，y＝1/112，所以甲做42天就做了工程的一半，乙就要56天来完成另一半。

  • 第12题：

    单选题
    有甲、乙两项工程，张师傅单独完成甲工程需要9天，单独完成乙工程需要12天；王师傅单独完成甲工程需要3天，单独完成乙工程需要15天。如果两人合作完成这两项工程，最少需要（）天。
    A

    8

    B

    10

    C

    12

    D

    14


    正确答案： A
    解析： 暂无解析

  • 第13题：

    师徒两人加工一批零件，由师傅单独做需37小时，徒弟每小时能加工30个零件，现由师徒两人同时加工，完成任务时，徒弟加工的个数是师傅的 ，这批零件共有( )个。

    A.2060

    B.2004

    C.1998

    D.2001


    正确答案：C
    C〔解析〕 徒弟每小时加工零件数是师傅的 ，师傅每小时加工零件30÷ (个)。这批零件共有：30÷ ×37＝1998（个）。

  • 第14题：

    师徒三人合作承包一项工程，8天能够全部完成。已知师傅独做所需的天数与两个徒弟合作所需要的天数相等，而师傅与乙徒弟合作所需的天数的4倍与甲徒弟单独完成所需的天数相等，问乙徒弟单独完成所需的天数是多少天?

    A．40天

    B．30天

    C．80/3天

    D．70/3天


    正确答案：C
    [答案] C。解析：设总工作量为“1”，徒弟甲、徒弟乙、师傅的工效分别为a、b、c。(a+b+c)×8=1,a+b=c,4a=b+c，解得b=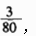所以徒弟乙单独完成所需的天数为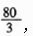选C。

  • 第15题：

    甲、乙、丙三人共同完成一项工程，他们的工作效率之比是5:4:6，先由甲、乙两人合作6天，再由乙单独做9天，
    完成全部工程的60%，若剩下的工程由丙单独完成，则丙所需要的天数是?

    A.10
    B.12
    C.9
    D.15

    答案：A
    解析：
    直接赋效率，已完成6*（5+4）+4*9=90，占60%，说明还剩60的工作量，60/6=10

  • 第16题：

    一件工程，甲乙两人合作３６小时完成，乙丙两人合作45小时完成，甲丙两人合作要60小时完成，问甲单独做需要多少小时完成？

    A.72
    B.75
    C.81
    D.90

    答案：D
    解析：
    我们设总的工作量是天数的最小公倍数，即180（36、45、60的最小公倍数），同时，设甲乙丙的工作效率分别是XYZ。题目说“甲乙两人合作36天完成”，说明甲乙合作一天的效率就是5（180÷36），根据“乙丙两人合作45天完成”，说明乙丙合作一天的效率就是4（180÷45），根据“甲丙两人合作要60天完成”，说明甲丙合作一天的效率就是3（180÷60）。所以可以列方程：
    X＋Y＝5，Y＋Z＝4，X＋Z＝3
    解方程得：X＝2，也就是甲单独做的工作效率是2，那么已知总的工作量为180，所以甲独 做需要90（180÷2）天完成。

  • 第17题：

    现由甲、乙、丙三人完成一项工程，如果由甲、乙两人合作，需要12小时完成；如果由乙、丙两人合作，需要l0小时完成；如果甲、乙、丙三人合作，需要6小时才能完成，则这项工程如果全部由甲单独完成，所需小时数为（　　）。

    A.15
    B.18
    C.20
    D.25

    答案：A
    解析：
    由题意知，甲、乙、丙三人合作需6小时完成，乙、丙两人合作需10小时完成，则甲单独
    {图}

  • 第18题：

    某工程甲单独做50天可以完成，乙单独做75天可以完成：现两人合作，但中途乙因事离开了几天，最后一共花了40天把这项工程做完，则中途乙离开了（）天。


    A. 15
    B. 16
    C. 22
    D. 25

    答案：D
    解析：
    解题指导： 设乙离开X天。则有方程：（40-X）（1/50+1/75）+1/50*X=1。可以算X=25。故答案为D。

  • 第19题：

    有一项工程，甲、乙、丙合作一天完成了工程的5/6，已知甲、乙、丙单独完成这项工程所用时间均为整数天数，且甲单独完成这项工程所用天数大于乙，乙所用天数大于丙，问甲、乙合作完成整个工程需要几天？

    A.3
    B.4
    C.5
    D.6

    答案：A
    解析：
    第一步，本题考查工程问题，属于时间类，用赋值法解题。
    第二步，结合题意赋总量为12，由“甲、乙、丙合作一天完成了工程的”，可知效率有：甲＋乙＋丙＝12×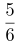＝10①，由“甲、乙、丙单独完成这项工程所用时间均为整数天数”，可得：12÷甲 ②、12÷乙③、12÷丙④均为整数，由②③④可得甲、乙、丙效率可能的取值为1、2、3、4、6等，由①及“甲单独完成这项工程所用天数大于乙，乙所用天数大于丙”，得效率：甲＝1，乙＝3，丙＝6满足题意。
    第三步，甲、乙合作完成整个工程需要＝3（天）。
    因此，选择A选项。

  • 第20题：

    某项工程，甲单独完成比乙单独完成快15天。现两人合作，5天后乙因事退出，甲又工 作了 3天完成了工程。问若甲、乙轮流做这项工程，多少天可以完成？

    a.12 b.15 c.17 d.20


    答案：B
    解析：

  • 第21题：

    有一项工程，甲单独做要36天完成，乙单独做要30天完成，丙单独做要48天完成。现在由甲、乙、丙三人同时做，在工作期间，丙休息了整数天，而甲和乙一直工作至完成，最后完成这项工程也用了整数天，问丙休息了几天？



    A.8
    B.9
    C.10
    D.11

    答案：D
    解析：

  • 第22题：

    案例：阅读下列有关“_元一次方程的实践与探索”教学片段。
    (多媒体展示)学校需要制作一块广告牌，请来两名工人。已知师傅单独完成需4天，徒弟
    单独完成需6天，两人合作需要几天完成
    解：设两人合作需要x天完成，根据题意列方程：
    解方程．得x=2．4。
    答：师徒两人合作需要2．4天完成任务。
    师：同学们对本题还有疑问么
    生：没有了!
    (情境拓展)
    师：真没有了 同学们想不想试着提出其他的问题来考考大家呢 如果想，请把问题写下来。
    教师的话引起了学生们的兴趣，学生个个跃跃欲试。
    稍后。教师在整理学生们的问题的过程中，发现有的学生按照教科书的提示出了这样一个
    问题。
    (1)学校需要制作一块广告牌，请来两名工人。已知师傅单独完成需4天，徒弟单独完成需6天．一人先做一天再和另一人合作，需几天完成
    生1：这个问题简单，把一人先做的量从总量中扣掉不就行了。
    师：你的想法很好!
    生2(迫切地举手)：老师，这道题出错了!问题说“一人先做”，可是没说哪个人先做啊。
    生3：对，可能是师傅先做，也可能是徒弟。所以我们得分两种情况来解决这个问题!
    生3的回答赢得了师生们热烈的掌声，解答过程略。)
    师：老师想把这个问题略加改动，还有信心挑战吗
    生(齐声)：有!
    (多媒体展示)
    (2)学校需要制作一块广告牌，请来两名工人。已知师傅单独完成需4天，徒弟单独完成需6天．两人先合作一天再一人单做，几天完成
    很快．不少同学积极举手，脸上露出自信的表情。
    生4：我发现问题(1)是先独做再合作，而问题(2)则正好相反。所以只要将两人合作的工作量扣掉就可以了。
    生5：跟问题(1)类似，我们也要分两种情况解决。
    师(a-出欣慰的笑容)：／两4-#-．-"同学的分析太精彩了!看来大家已经感受到了数学中的分类讨论思想。现在老师看看同学4r1-还提出了什么问题。
    此时学生情绪高涨，期待老师展示下一个题目。
    (多媒体展示)
    (3)学校需要制作一块广告牌，请来两名工人。已知师傅单独完成需4天，徒弟单独完成需6天，两人合作，完成后共得报酬l 000元，如果按个人完成的工作量计算报酬，那么该如何分配
    生6(按捺不住兴奋)．这个问题太简单了，师傅和徒弟的工作效率之比是6：4，所以师傅应得600元，徒弟应得400元。
    师：你能灵活地应用师徒二人的工作效率之间的关系来解答此题，思维很敏捷呀!
    师(故作困惑)：现由徒弟先做l天，再由两人合作，完成后共得报酬450元。如果按个人完成的工作量计算报酬，那么又该如何分配
    学生们认真思考着……
    在问题(3)的启发下，许多学生对本题予以了正确解答。
    问题：
    (1)分析案例中教学过程的特点：
    (2)根据案例内容，结合你的教学经历，说明创造性地使用数学教科书的原则。


    答案：
    解析：
    (1)“工程问题”虽然在小学就涉及到了，但仍然是七年级学生难以掌握的问题。这个教学片段以“工程问题”中的基本例题为“根基”，教师有目的、有意识地筛选出学生们自己提出的问题进行解决：从“两人合作”到“一人先做再合作”到“先合作再一人单做”再到“报酬的合理分配”。这四个问题，采用“给出情境．让学生参与”的教学方法，对教科书中的例题进行了合理的变形、转化、拓展与综合，深入挖掘其中潜在的数学思想方法，并揭示其丰富内涵。不但有利于学生掌握基础知识、激发学生的学习兴趣、发挥学生的想象力和创造精神，而且对培养学生的应变能力、开拓思维，提高学生对数学建模思想的认识等都是很有益的。这种训练．也符合目前中考命题“源于教科书、高于教科书”的原则，与素质教育要求的“培养学生的创新能力”相吻合。
    (2)①摒弃陈旧的教材使用观。童话大王郑渊洁说：“用一模一样的教材去教育不一样的孩子．简直是童话。”教科书是教学活动的最主要材料。在新一轮课改环境下，虽然教科书越来越科学化，但是，有的教师往往只是照本宣科，教学活动缺乏创造性，并不能最大限度地发挥教科书的作用。作为教师，一定要转变旧的教材使用观，结合学生的实际情况，把教科书作为传授知识锻炼能力的依托，变完全依赖教科书为创造性地使用教科书，为学生积极主动地探求知识创设良好的教学情境。
    ②紧扣课程标准。教师要深入研究课程标准，然后结合教学实际，适当对教科书进行取舍整合。教科书是课堂教学的依托，是在国家课程标准指导下经教育专家编写的具有很强科学性的教学载体，不要轻易否定。教师创造性地使用教科书，务必要以课程标准为出发点和立足点，加强对教科书的深入钻研和正确把握，熟谙教学目标，明确重难点，理清知识脉络，力争做到有的放矢，真正实现教科书的创新，为学生服务。
    ③抓住学生这个主体。一切教学活动必须落实到学生这一主体。教师要创造性地使用教科书，必须根据学生的实际而定，教师只是整个教学工作的“导演”，由于每个教师有每个教师的特长，所以，不同的教师会从不同的角度挖掘教科书的内涵，创造性地使用教科书。有的教师善于使用现代教学手段，教学效果好；有的教师擅长用艺术来组织教学．效果也不错。如教学“直线与圆的位置关系”时运用一首占诗“大漠孤烟直，长河落日圆”来引课，让学生进行形象思维，通过这种意境抽象出数学模型，初步形成直线与圆的三种位置关系，这是对教科书的拓展。效果很不错。
    ④根据具体教学情境活用课程资源。在具体的教学情境中．教师要根据出现的预想之外的许多问题灵活处理教科书，引导学生向教科书的意图靠近，为学生创造良好的学习情境。同时，依据教学环境确定教科书的内容取舍是必要的。课程资源非常广泛，如报刊、电视及日常生活都可以成为课程资源，创造性地使用教科书就必须灵活运用课程资源．从而拓宽学生学习的空间。实现开放的教学模式。

  • 第23题：

    单选题
    有一项工程，由甲、乙按天轮流做，如果从甲开始轮流做下去，正好用整数天完工；如果从乙开始轮流做下去，则需多耗时半天才能完成。已知乙单独完成这项工程需17天，那么，甲单独完成这项工程需多少天？（）
    A

    8

    B

    8.5

    C

    9

    D

    9.5


    正确答案： A
    解析： 暂无解析

相关内容